The data cleansing phase alone is not sufficient to ensure the accuracy of the machine learning, when noise / bias exists in input data. The lean six sigma variance reduction can improve the accuracy of machine learning results.
By Joseph Chen, Senior Management and Architect in BI, Data Warehouse, Six Sigma, and Operations Research.
I have been using Lean Six Sigma (LSS) to improve business processes for the past 10+ year and am very satisfied with its benefits. Recently, I’ve been working with a consulting firm and a software vendor to implement a machine learning (ML) model to predict remaining useful life (RUL) of service parts. The result which I feel most frustrated is the low accuracy of the resulting model. As shown below, if people measure the deviation as the absolute difference between the actual part life and the predicted one, the resulting model has 127, 60, and 36 days of average deviation for the selected 3 parts. I could not understand why the deviations are so large with machine learning.
After working with the consultants and data scientists, it appears that they can improve the deviation only by 10% through data cleansing. This puzzles me a lot. To me, such deviation, even after the 10% improvement, still renders the forecast useless to the business owners. This forces me to ask myself the following questions:
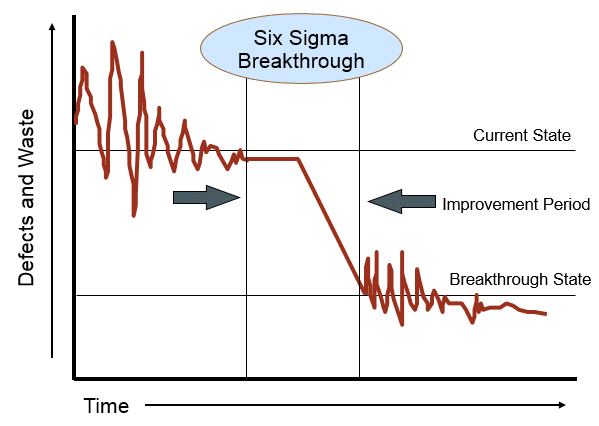
The objective of the lean six sigma (LSS) is to improve process performance by reducing its variance. The variance is defined as the sum squared errors (differences) between the LSS actual and forecast measures. The result of the LSS essentially is a statistical function (model) between a set of input / independent variables and the output / dependent variable(s), as show in the chart below.
By identifying the correlations between the input and output variables, the LSS model tells us how we can control the input variables in order to move the output variable(s) into our target values. Most importantly, LSS also requires the monitored process to be “stable”, i.e., minimizing the output variable variance, by minimizing the input variable variance, in order to achieve the so called “breakthrough” state.
As the chart below shows, if you get to your target (center) alone without variance control (the spread around the target in the left chart), there is no guarantee about the target you have achieved; if you reduce the variance without getting to the target (right chart), you miss your target. Only by keeping the variance small and center, LSS is able to ensure the process target is reached with precise precision and with a sustainable and optimal process performance. This is the major contribution of LSS.
